2. Softmax 回归
2. Softmax 回归 (LLN for Classification)
1. Softmax 回归与分类问题
-
Softmax 回归:是一种用于多类别分类的线性模型。输出层是每个类别的得分(logits),通过 softmax 函数变成概率分布。
-
回归 vs. 分类
- 回归:预测连续值,输出是实数域
。
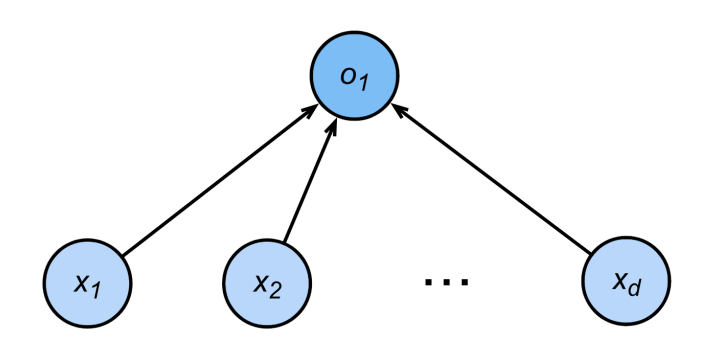
- 分类:预测离散标签,输出为各类别的概率或置信度。
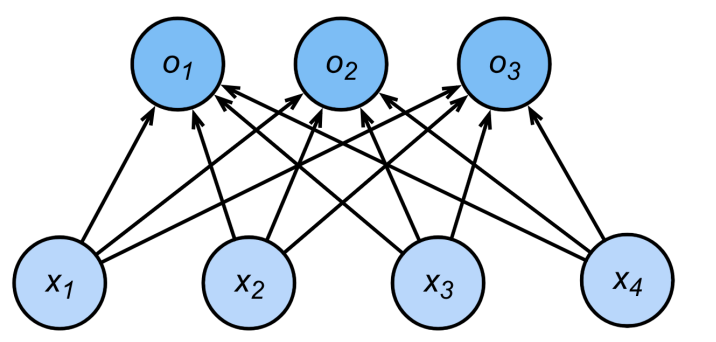
- 回归:预测连续值,输出是实数域
-
多类别分类建模流程:
- 对类别进行一位有效编码(one-hot encoding):
其中: - 输出原始分数(logits):
- 预测类别:
- 使用Softmax函数将logits转为概率分布:
- 对类别进行一位有效编码(one-hot encoding):
-
类别区分的本质:
- 分类模型需保证正确类别的得分高于其他类别,可以用如
这样的条件提升鲁棒性(了解即可,主流做法还是用Softmax+交叉熵)。
- 分类模型需保证正确类别的得分高于其他类别,可以用如
- 目标 :
- 在分类任务中,模型需要能够明确区分正确的类别和其他类别,确保预测结果具有较高的置信度。
- 这种区分能力可以通过增加“真正的类”与其他类之间的得分差距来实现。
- 无检验比例 :
表示在输出层上,正确类 的得分 应该比其他类 的得分 至少高出一个预设的阈值 。这有助于提高分类的鲁棒性和准确性。
- 有检验比例 :
- 使用 Softmax 函数 将模型的原始输出
转换为概率分布 ,确保所有类别的概率非负且总和为 1。
- 使用 Softmax 函数 将模型的原始输出
2. Softmax 和交叉熵损失
-
Softmax函数 保证输出为概率分布(非负,总和为1)。
-
交叉熵损失(Cross-Entropy Loss) 常用于衡量真实分布
与预测分布 的差异: - 对于独热标签
,损失可写为:
- 对于独热标签
-
交叉熵梯度(对logits的导数):
-
one-hot编码说明:
- 独热编码向量长度等于类别数,只有一个元素为1,其余为0。
- 例:三分类时,
可能为
-
仿射函数(Affine function):
:权重矩阵(线性变换) :偏置(平移项)
3. 常见损失函数对比(回归用)
- 均方误差(MSE):
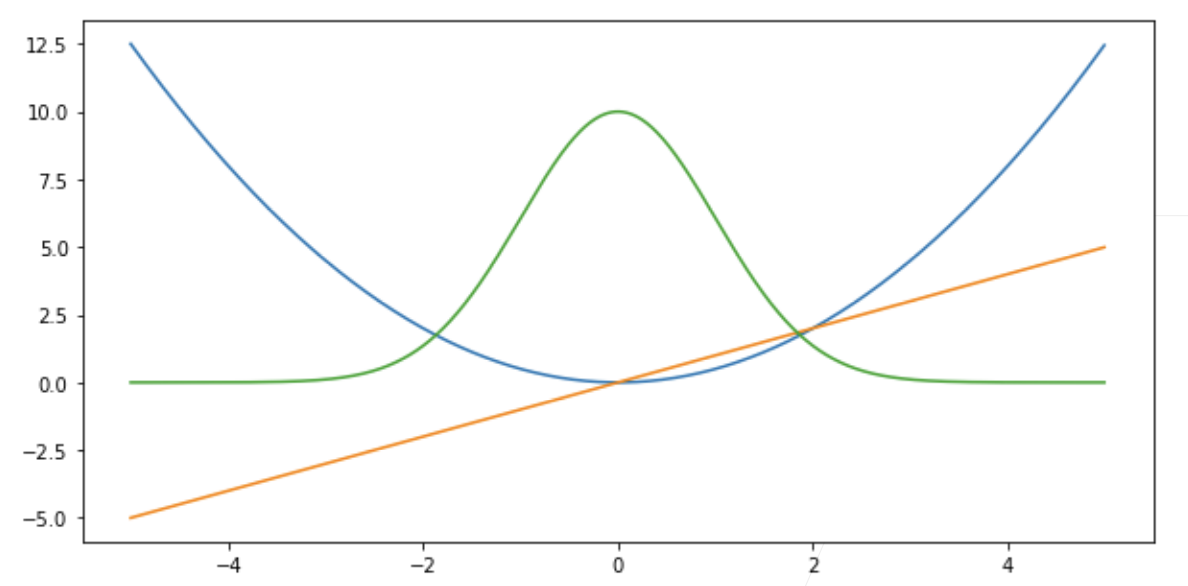
- 绝对值损失(MAE):
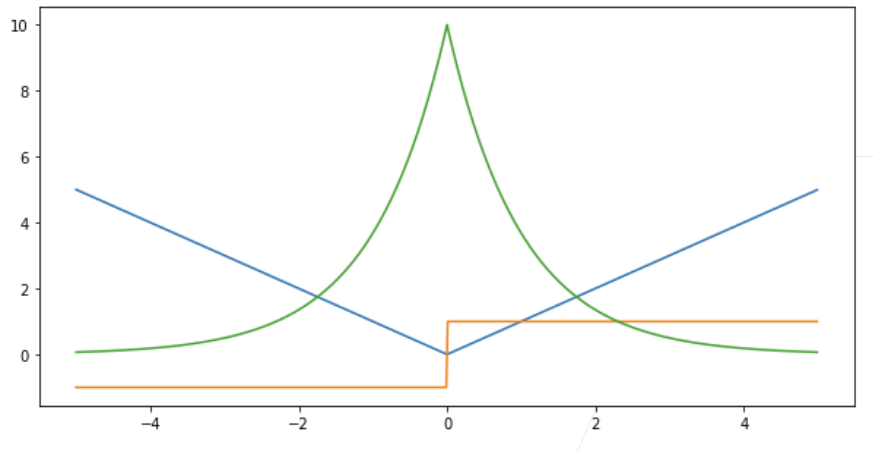
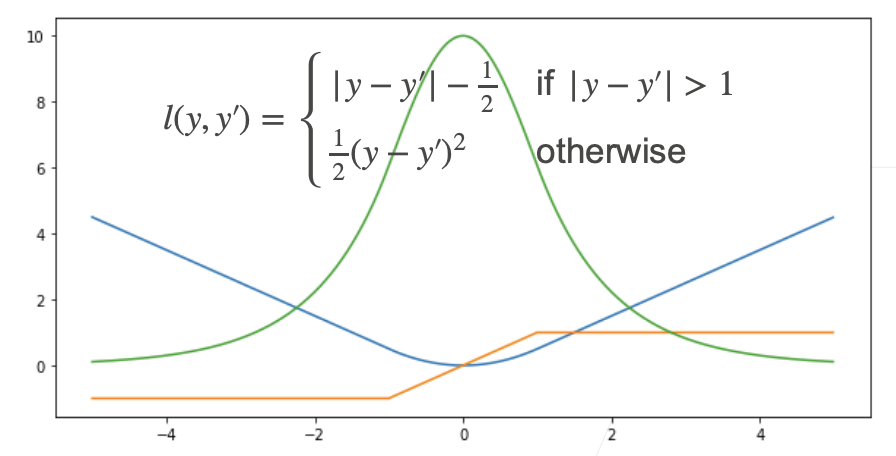
- Huber 损失(Robust loss):
4. 总结
- Softmax回归是多类分类的线性模型,输出通过Softmax归一化为概率分布。
- 核心损失为交叉熵,反映模型预测分布与真实标签分布的距离。
- one-hot编码是分类任务常用标签表示方式。
- Softmax输出让所有类别概率加和为1,适合分类场景。
参考资料
“觉得不错的话,给点打赏吧 ୧(๑•̀⌄•́๑)૭”

微信支付

支付宝支付
2. Softmax 回归
http://neurowave.tech/2025/04/22/10-2-LNN-softmax/