7. 数值稳定

1. 数值稳定性

• 神经网络的梯度

  • 考虑一个有 $d$ 层的神经网络：
  $${\mathbf{h}}^t=f_t({\mathbf{h}}^{t-1})\text{and}y=\ell \cdot f_d\cdot ...\cdot f_1(\mathbf{x})$$
  • 计算损失 $\ell$ 关于参数 ${\mathbf{W}}_t$ 的梯度：
  $$\frac{\partial \ell }{\partial {\mathbf{W}}_t}=\frac{\partial \ell }{\partial {\mathbf{h}}^d}\cdot \frac{\partial {\mathbf{h}}^d}{\partial {\mathbf{h}}^{d-1}}\cdot ...\cdot \frac{\partial {\mathbf{h}}^{t+1}}{\partial {\mathbf{h}}^t}\cdot \frac{\partial {\mathbf{h}}^t}{\partial {\mathbf{W}}_t}$$
  • 链式法则：反向传播时，多个层的梯度相乘，导致数值可能急剧增大或减小。

• 梯度爆炸与梯度消失

  • 梯度爆炸（Gradient Explosion）：参数更新过大，导致模型权重数值不断增大，最终发生溢出。
    • 示例：${1.5}^{100}\approx 4\times {10}^{17}$。
  • 梯度消失（Gradient Vanishing）：随着反向传播的进行，梯度变得非常小，导致无法有效更新模型权重。
    • 示例：${0.8}^{100}\approx 2\times {10}^{-10}$。
  • 常见诱因：层数过深、激活函数/初始化不当、学习率失控。

• 激活函数的影响

  • ReLU ：一般能缓解梯度消失，但依然可能导致爆炸。

    $$\sigma (x)=max(0,x)\text{and}{\sigma }^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ 0,& \text{otherwise}\end{array}$$
    • 如果 $d-t$ 较大，梯度会变得非常大，造成数值爆炸。

  • Sigmoid： 在区间两端梯度非常小，极易导致梯度消失。

    $$\sigma (x)=\frac{1}{1+e^{-x}}\text{and}{\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$$

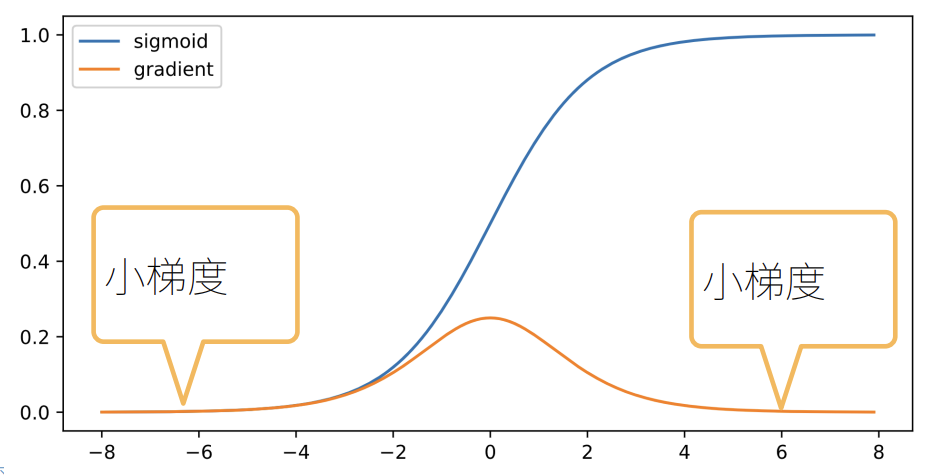
• 计算中常见的数值不稳定

  • 数值溢出：参数值过大或过小，超出数值类型（如16位浮点数）的表示范围。
  • 学习率敏感：学习率过大→爆炸，过小→不收敛
  • 深层网络更易中招：链式乘积n次，深度越大，越不稳定。

• 例子：在MLP中，前向传播和反向传播都受到激活函数的影响。使用ReLU：爆炸风险更大。使用Sigmoid：消失风险更大。

1. 使用ReLU：

$$\begin{array}{rl}{f}_t(h^{t-1})& =\sigma (W^t{h}^{t-1}),\\ \frac{\partial h^t}{\partial h^{t-1}}& =\text{diag}({\sigma }^{\prime }(W^t{h}^{t-1}))(W^t{)}^T\end{array}$$

2. 使用Sigmoid时：

$$\prod _{i=t}^{d-1}\frac{\partial {\mathbf{h}}^{i+1}}{\partial {\mathbf{h}}^i}=\prod _{i=t}^{d-1}\text{diag}({\sigma }^{\prime }({\mathbf{W}}^i{\mathbf{h}}^{i-1}))({\mathbf{W}}^i{)}^T$$

2. 让训练更加稳定

• 目标：让梯度值在合理的范围内（例如 $[1\times {10}^{-6},1\times {10}^3]$）。
  1. 将乘法变加法：例如：ResNet、LSTM
  2. 归一化：梯度归一化、梯度裁剪
  3. 合理的，权重初始化、激活函数

MLP中的例子

• 目标：让每一层的输出和反向梯度的方差都是常数，避免数值爆炸或消失。
  • 每层输出和梯度都看作随机变量，要求均值为0、方差为常数（独立同分布）。

$$\begin{array}{|cc|}\hline \mathbf{\text{正向传播}}& \mathbf{\text{反向传播}}\\ \mathbb{E}[h_i^t]=0& \mathbb{E}\left[\frac{\partial \ell }{\partial h_i^t}\right]=0\\ \text{Var}[h_i^t]=a& \text{Var}\left[\frac{\partial \ell }{\partial h_i^t}\right]=b\mathrm{\forall }i,t\\ \hline\end{array}$$

1. 假设：$w_{i,j}^t$ 是独立同分布（i.i.d.），且满足：

   • $\mathbb{E}[w_{i,j}^t]=0,\text{Var}[w_{i,j}^t]={\gamma }_t$
   • $h_i^{t+1}$ 独立于 $w_{i,j}^t$

2. 没有激活函数：$h^t=W^t{h}^{t-1}$，其中 $W^t\in {\mathbb{R}}^{n_t\times n_{t-1}}$。

• 正向方差：

$$\begin{array}{rl}\mathbb{E}[h_i^t]& =\mathbb{E}[\sum _j{w}_{i,j}^t\cdot h_j^{t-1}]=\sum _j\mathbb{E}[w_{i,j}^t]\cdot \mathbb{E}[h_j^{t-1}]=0\\ \text{Var}[h_i^t]& =\mathbb{E}[(h_i^t{)}^2]-\underset{=0}{\underbrace{(\mathbb{E}[h_i^t]{)}^2}}=\mathbb{E}\left[{(\sum _j{w}_{i,j}^t\cdot h_j^{t-1})}^2\right]\\ & =\sum _j\mathbb{E}[(w_{i,j}^t{)}^2]\cdot \mathbb{E}[(h_j^{t-1}{)}^2]+\sum _{j\ne k}\underset{=0}{\underbrace{\mathbb{E}[w_{i,j}^t\cdot w_{i,k}^t]}}\cdot \mathbb{E}[h_j^{t-1}\cdot h_k^{t-1}]\\ & =\sum _j\text{Var}[w_{i,j}^t]\cdot \text{Var}[h_j^{t-1}]\\ & =n_{t-1}\cdot {\gamma }_t\cdot \text{Var}[h_j^{t-1}]\end{array}$$

• 反向传播梯度：

$$\begin{array}{rl}\frac{\partial \ell }{\partial h_i^{t-1}}& =\frac{\partial \ell }{\partial h^t}{W}^t\\ \Rightarrow \mathbb{E}\left[\frac{\partial \ell }{\partial h_i^{t-1}}\right]& =0\\ \text{Var}\left[\frac{\partial \ell }{\partial h_i^{t-1}}\right]& =n_t\cdot {\gamma }_t\cdot \text{Var}\left[\frac{\partial \ell }{\partial h_j^t}\right]\end{array}$$

• $n_{t-1}{\gamma }_t=1$
• 为保证所有层的方差一致，理想要求 $n_{t-1}{\gamma }_t=1$ 且 $n_t{\gamma }_t=1$，但实际很难同时满足。

3. 常用：Xavier初始化（针对深度网络）
   • Xavier初始化可以避免梯度爆炸或消失。
   • Xavier初始化：适用于深度神经网络，通过平衡层输入输出的方差，使梯度在训练过程中更加稳定。
     • ${\gamma }_t(n_{t-1}+n_t)/2=1$ ; ${\gamma }_t=\frac{2}{nt-1+n_t}$
     • 正态分布：$\mathcal{N}(0,\sqrt{2/(n_{t-1}+n_t)})$
     • 均匀分布：$\mathcal{U}(-\sqrt{6/(n_{t-1}+n_t)},\sqrt{6/(n_{t-1}+n_t)})$
     • note：$U(-a,a)$ 的方差为 $a^2/3$。

3. 结论

• 梯度爆炸和梯度消失是深度神经网络常见的数值稳定性难题，尤其在网络层数增加后更突出。
• 主要对策有三条：
  1. 权重初始化要科学：优先选用Xavier或He初始化，降低数值极端波动风险。
  2. 归一化机制要用好：如Batch Normalization，让每一层的输出和梯度方差都在合理范围，防止异常扩散或消失。
  3. 激活函数要选对：避免Sigmoid等极易导致梯度消失的激活函数，推荐ReLU及其变体。
• 训练过程中还需关注学习率调整，权重初始化和归一化相结合才能最大程度保证数值稳定。

参考资料

• 李沐《手动深度学习》：数值稳定
• Bilibili：数值稳定