LLaMa（书）

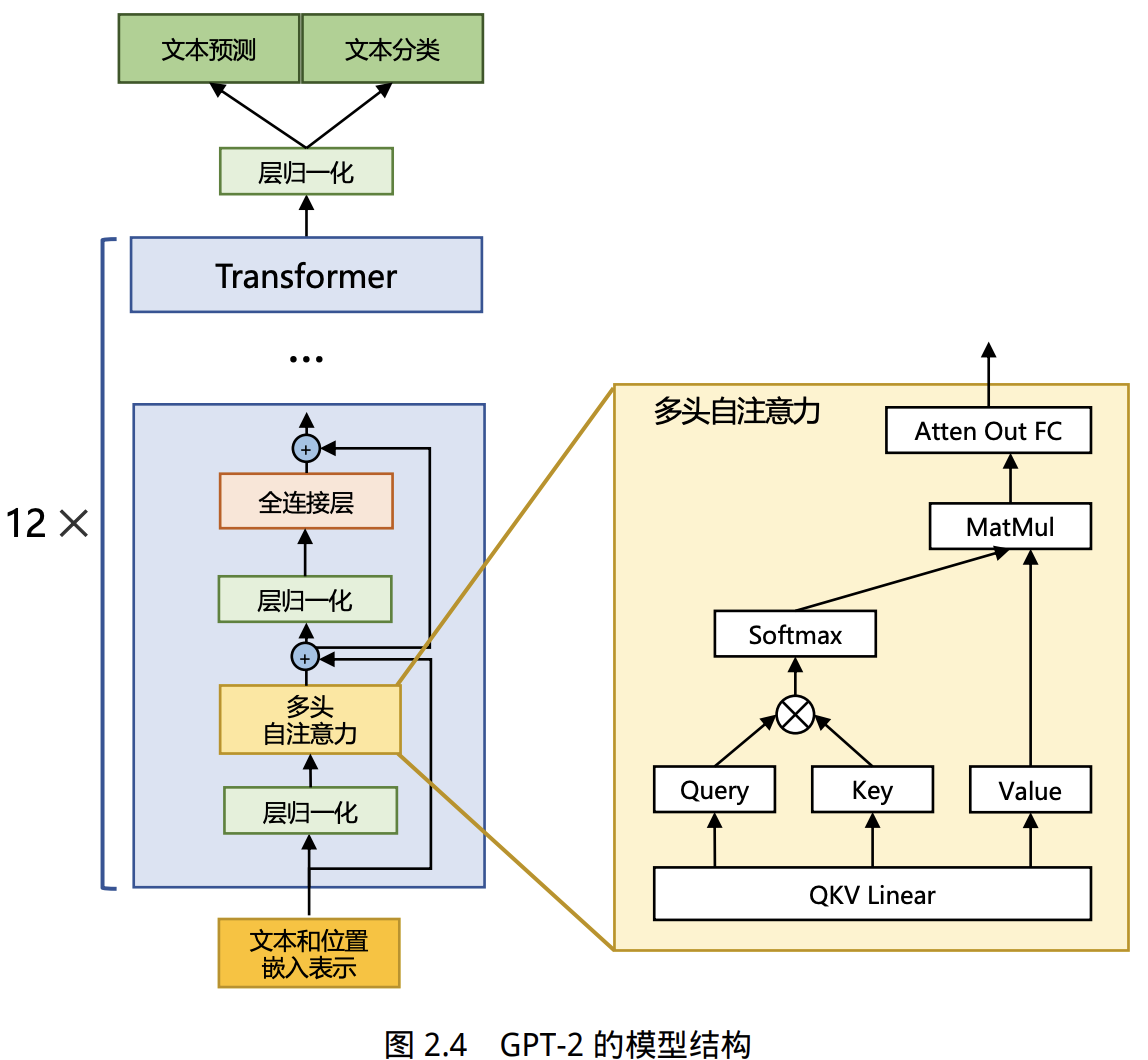
• 绝大多数大语言模型采用类似GPT的自回归Transformer解码器架构，各模型在位置编码、归一化、激活函数等细节有所不同。
• GPT-3未开源，社区有OPT等开源复现；MetaAI基于GPT-3架构开源了LLaMA，效果优秀。
• OpenAI的GPT-3后续模型未再开源。后续结构分析主要参考LLaMA。

LLaMA采用的Transformer结构与GPT-2类似，主要改进有：

• 前置层归一化（Pre-normalization），使用RMSNorm归一化函数
• 激活函数换为SwiGLU
• 采用旋转位置嵌入（RoPE）

1. RMSNorm归一化函数

• RMSNorm归一化函数（Root Mean Square Layer Normalization）常用于如LLaMA、GPT-2的前置归一化（pre-norm）结构。
• 与LayerNorm区别：RMSNorm不做均值减法，仅按方差归一化。

RMSNorm计算公式

对于输入向量 $\mathbf{a}=(a_1,a_2,...,a_n)$，

• 1. 计算均方根（Root Mean Square, RMS）：

  $$\text{RMS}(\mathbf{a})=\sqrt{\frac{1}{n}\sum _{i=1}^n{a}_i^2}$$

• 2. 归一化每个分量：

  $${\overline{a}}_i=\frac{a_i}{\text{RMS}(\mathbf{a})}$$

• 3. 可学习仿射变换：

  $${\overline{a}}_i=\frac{a_i}{\text{RMS}(\mathbf{a})}{g}_i+b_i$$

  其中 $g_i$ 为可学习的缩放因子，$b_i$ 为可学习的偏置（常用$g$为向量，$b$可选）。

2. SwiGLU 激活函数

• SwiGLU 激活函数的提出者及应用：Shazeer 提出，在 PaLM 等模型中广泛应用，取得不错效果。

• 与 ReLU 的对比：相比 ReLU，SwiGLU 在大部分评测中提升明显。

• 在 LLaMA 中的使用方式：全连接层采用 SwiGLU 激活函数，具体公式如下：

  $$\begin{array}{rl}{\text{FFN}}_{\text{SwiGLU}}(\mathbf{x},\mathbf{W},\mathbf{V},W_2)& =\text{SwiGLU}(\mathbf{x},\mathbf{W},\mathbf{V})W_2\\ \text{SwiGLU}(\mathbf{x},\mathbf{W},\mathbf{V})& ={\text{Swish}}_{\beta }(\mathbf{x}\mathbf{W})\otimes \mathbf{x}\mathbf{V}\\ {\text{Swish}}_{\beta }(x)& =x\cdot \sigma (\beta x)\end{array}$$
  • 其中 $\sigma (x)$ 为 Sigmoid 函数

• Swish 激活函数 $\beta$ 参数影响

  • 当 $\beta \to 0$ 时，Swish 接近线性函数 $y=x$
  • 当 $\beta \to \mathrm{\infty }$ 时，Swish 接近 ReLU
  • 当 $\beta =1$ 时，Swish 光滑且非单调

• 工程实现：HuggingFace 的 transformers 库用 SiLU 代替 Swish

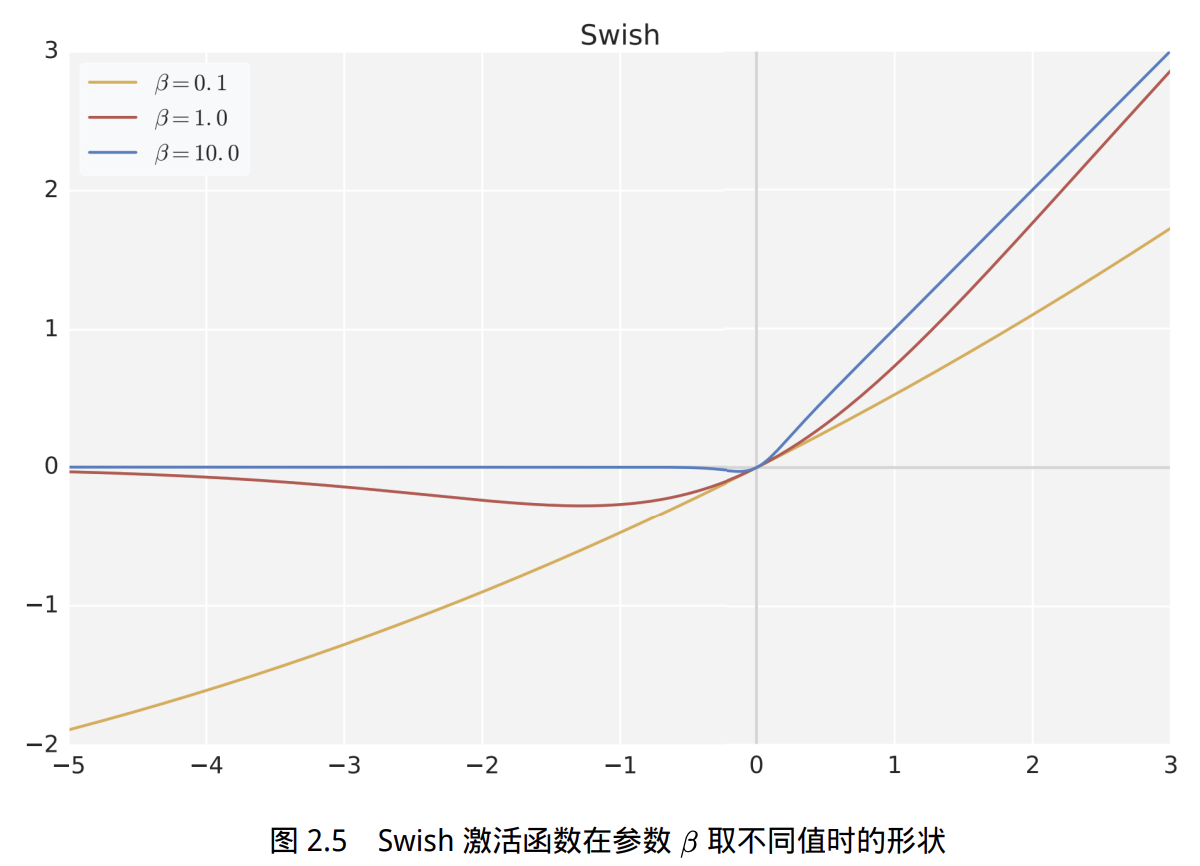
• 曲线对比了 $\beta =0.1$、$\beta =1.0$、$\beta =10.0$ 三种情况。
• $\beta$ 越小（如 $\beta =0.1$，黄色），曲线越接近一条斜直线，即接近 $y=x$，表现为线性函数。
• $\beta =1.0$（红色）时，曲线介于线性和ReLU之间，光滑但非单调。
• $\beta$ 很大（如 $\beta =10.0$，蓝色），曲线在 $x>0$ 时和 $y=x$ 很接近，$x<0$ 时趋于零，形状接近 ReLU 激活函数。

3. RoPE（Rotary Position Embedding）

1. 基本思想：用旋转式位置嵌入（RoPE）代替绝对位置编码。RoPE 利用复数的几何意义，实现相对位置编码。

2. 基本形式
   通过函数 $f$ 对查询 $\mathbf{q}$、键 $\mathbf{k}$ 添加绝对位置信息：

   $${\tilde{\mathbf{q}}}_m=f(\mathbf{q},m),{\tilde{\mathbf{k}}}_n=f(\mathbf{k},n)$$

3. 复数表示的 RoPE：这个变换几何上等价于对向量进行旋转。

   $$f(\mathbf{q},m)=R_f(\mathbf{q},m)e^{i{\theta }_{f(\mathbf{q},m)}}=\parallel \mathbf{q}\parallel e^{i(\theta (\mathbf{q})+m\theta )}=\mathbf{q}{e}^{im\theta }$$

4. 二维矩阵形式

   $$f(\mathbf{q},m)=\left(\begin{array}{cc}\cos (m\theta )& -\sin (m\theta )\\ \sin (m\theta )& \cos (m\theta )\end{array}\right)\left(\begin{array}{c}{q}_0\\ q_1\end{array}\right)$$

5. 高维拼接形式：任意偶数维的 RoPE 可表示为多个二维旋转块的拼接：

   $$f(\mathbf{q},m)=\underset{R_d}{\underbrace{\left(\begin{array}{ccccc}\cos (m{\theta }_0)& -\sin (m{\theta }_0)& & & \\ \sin (m{\theta }_0)& \cos (m{\theta }_0)& & & \\ & & \cos (m{\theta }_1)& -\sin (m{\theta }_1)& \\ & & \sin (m{\theta }_1)& \cos (m{\theta }_1)& \\ & & & & \ddots \end{array}\right)}}\left(\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right)$$

6. 高效计算：由于 $R_d$ 是多个 2×2 块的对角拼接，具备稀疏性，可用按位乘（$\otimes$）操作进一步提升计算速度。

参考资料

• 《大语言模型：从理论到实践（第二版）》-- 张奇、桂韬、郑锐、黄萱菁